https://www.acmicpc.net/problem/12015
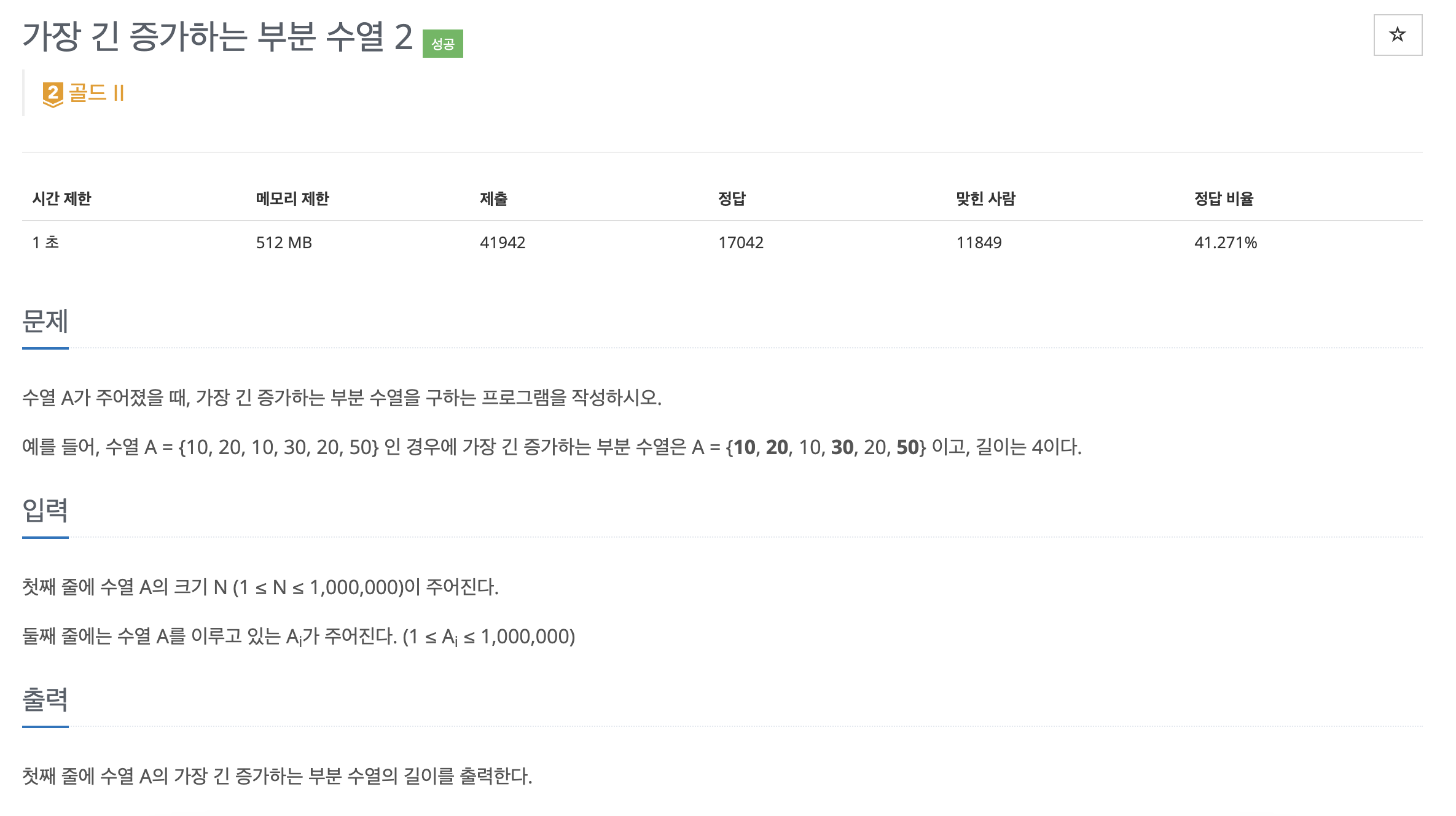
12015번: 가장 긴 증가하는 부분 수열 2
첫째 줄에 수열 A의 크기 N (1 ≤ N ≤ 1,000,000)이 주어진다. 둘째 줄에는 수열 A를 이루고 있는 Ai가 주어진다. (1 ≤ Ai ≤ 1,000,000)
www.acmicpc.net
풀이
기존의 dp로만 풀어주면 시간초과가 일어난다. dp풀이는 N^2의 시간 복잡도를 가지기 때문에
N의 크기가 최대 10^6이기에 1초를 넘어서는 시간초과가 일어난다.
그래서 이분탐색을 이용해서 풀어줘야하는 문제이다.
DP 코드(시간초과)
n = int(input())
arr = list(map(int, input().split()))
dp = [1 for i in range(n)]
for i in range(n):
for j in range(i):
if arr[i] > arr[j]:
dp[i] = max(dp[i], dp[j]+1)
print(max(dp))
이분탐색을 이용한 코드
# 12015번 가장 긴 증가하는 부분 수열 2
n = int(input())
nums = list(map(int, input().split()))
# 내가 관심이 있는건 수열에 새로운 숫자를 추가하기 위해서는
# 수열의 마지막 숫자의 크기만이 중요하다. 그 이전의 존재하는 숫자의 크기는 상관없다.
def bin_sec(target):
start = 0
end = len(dp)-1
while start <= end:
mid = (start+end) // 2
# 중복된 숫자가 들어왔을 경우 dp리스트에 원래 있던 자리에 그대로 넣어준다.
if dp[mid] == target:
return mid
elif dp[mid] > target:
end = mid - 1
else:
start = mid + 1
# 숫자를 넣기 적절한 위치
return start
dp = [nums[0]]
for i in nums:
if dp[-1] < i:
dp.append(i)
else:
idx = bin_sec(i)
dp[idx] = i
print(len(dp))출력결과

'백준 > 이분 탐색' 카테고리의 다른 글
| [백준] 1654번 랜선 자르기 - 파이썬 (0) | 2022.02.07 |
|---|
https://www.acmicpc.net/problem/12015
12015번: 가장 긴 증가하는 부분 수열 2
첫째 줄에 수열 A의 크기 N (1 ≤ N ≤ 1,000,000)이 주어진다. 둘째 줄에는 수열 A를 이루고 있는 Ai가 주어진다. (1 ≤ Ai ≤ 1,000,000)
www.acmicpc.net

풀이
기존의 dp로만 풀어주면 시간초과가 일어난다. dp풀이는 N^2의 시간 복잡도를 가지기 때문에
N의 크기가 최대 10^6이기에 1초를 넘어서는 시간초과가 일어난다.
그래서 이분탐색을 이용해서 풀어줘야하는 문제이다.
DP 코드(시간초과)
n = int(input())
arr = list(map(int, input().split()))
dp = [1 for i in range(n)]
for i in range(n):
for j in range(i):
if arr[i] > arr[j]:
dp[i] = max(dp[i], dp[j]+1)
print(max(dp))
이분탐색을 이용한 코드
# 12015번 가장 긴 증가하는 부분 수열 2
n = int(input())
nums = list(map(int, input().split()))
# 내가 관심이 있는건 수열에 새로운 숫자를 추가하기 위해서는
# 수열의 마지막 숫자의 크기만이 중요하다. 그 이전의 존재하는 숫자의 크기는 상관없다.
def bin_sec(target):
start = 0
end = len(dp)-1
while start <= end:
mid = (start+end) // 2
# 중복된 숫자가 들어왔을 경우 dp리스트에 원래 있던 자리에 그대로 넣어준다.
if dp[mid] == target:
return mid
elif dp[mid] > target:
end = mid - 1
else:
start = mid + 1
# 숫자를 넣기 적절한 위치
return start
dp = [nums[0]]
for i in nums:
if dp[-1] < i:
dp.append(i)
else:
idx = bin_sec(i)
dp[idx] = i
print(len(dp))출력결과

'백준 > 이분 탐색' 카테고리의 다른 글
| [백준] 1654번 랜선 자르기 - 파이썬 (0) | 2022.02.07 |
|---|
