
분할 정복(Divide and Conquer)을 사용한 거듭제곱 계산법은 수학적 문제 해결과 알고리즘 설계에서 매우 강력한 접근 방식입니다. 이 방법은 복잡해 보이는 문제를 더 작고 관리하기 쉬운 부분 문제로 나누고, 이를 재귀적으로 해결한 다음, 결과를 조합하여 최종 해답을 도출합니다. 특히, 거듭제곱 계산과 같은 수학적 연산에서 분할 정복 방법은 일반적인 반복 또는 직접 계산 방식보다 훨씬 더 효율적일 수 있습니다. 그 이유를 몇 가지 측면에서 설명해보겠습니다.
시간 복잡도의 개선
가장 직관적인 거듭제곱 계산 방법은 (a)를 (n)번 곱하는 것입니다. 이 방식의 시간 복잡도는 (O(n))입니다. 반면, 분할 정복을 사용한 거듭제곱 계산법은 (O(\log n))의 시간 복잡도를 가집니다. 이는 (n)이 커질수록 기존 방법에 비해 필요한 연산 횟수가 지수적으로 감소함을 의미합니다. 예를 들어, (2^{32})를 계산한다고 할 때, 직접 계산 방식은 32번의 곱셈을 필요로 하는 반면, 분할 정복 방식은 단 5번의 곱셈만을 필요로 합니다. 이는 계산 과정에서 필요한 리소스와 시간을 대폭 줄여줍니다.
메모리 사용의 최적화
분할 정복 방식은 추가적인 메모리 사용 없이 계산을 수행할 수 있습니다. 재귀적 구현에도 불구하고, 현대 컴퓨터의 스택 크기는 대부분의 거듭제곱 계산 요구를 충분히 수용할 수 있으며, 분할 정복 알고리즘의 깊이는 (O(\log n))에 불과하기 때문에, 깊은 재귀 호출로 인한 스택 오버플로우 문제가 발생할 가능성이 낮습니다.
코드의 간결성
분할 정복을 사용한 거듭제곱 계산법은 코드의 복잡성을 줄이는 데에도 기여합니다. 재귀적 접근 방식은 알고리즘의 구현을 명확하고 간결하게 만들어, 코드의 가독성과 유지 보수성을 향상시킵니다. 또한, 분할 정복 방식은 다양한 수학적 문제와 알고리즘에 적용 가능한 범용적인 접근법을 제공합니다.
결론
분할 정복을 사용한 거듭제곱 계산법은 계산의 효율성, 메모리 사용의 최적화, 그리고 코드의 간결성 측면에서 뛰어난 이점을 제공합니다. 이 방법은 특히 큰 숫자의 거듭제곱을 계산할 때 그 효율성이 두드러지며, 알고리즘의 성능을 크게 향상시킬 수 있습니다. 따라서 수학적 문제 해결과 소프트웨어 개발에서 분할 정복 방식의 거듭제곱 계산법을 적극적으로 활용하는 것이 바람직합니다
분할 정복을 사용한 거듭제곱을 구현하는 방법은 반복문과 재귀문이 있습니다.
반복문
def iterative_power(a, n):
result = 1
while n > 0:
# n이 홀수인 경우, 결과에 a를 곱하고 n을 하나 감소
if n % 2 == 1:
result *= a
n -= 1
# a를 제곱하고 n을 반으로 줄임
a *= a
n //= 2
return result재귀문
def recursive_power(a, n):
if n == 0:
return 1
elif n % 2 == 0:
half_power = recursive_power(a, n // 2)
return half_power * half_power
else:
half_power = recursive_power(a, (n-1) // 2)
return half_power * half_power * a
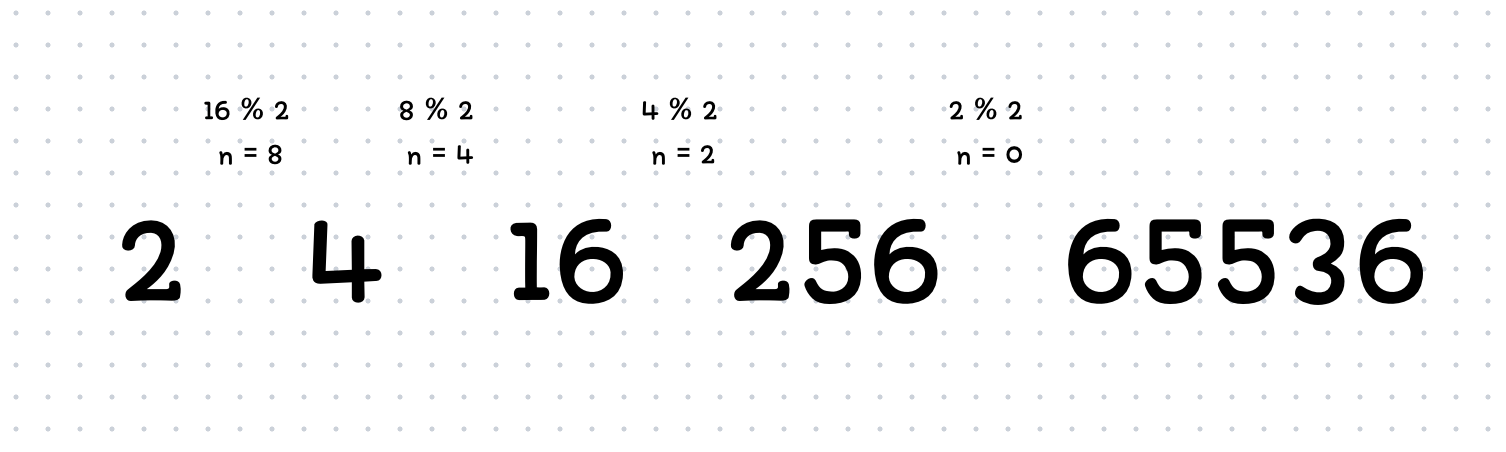
다음 예시는 2^16을 분할 정복을 활용하여 구해보는 과정입니다.(n = 16, a = 2)
분할정복에 의하면 a를 n을 2로 나눈 나머지가 0이 될 때까지 a 자신을 곱하게 만드는 것입니다.
다음과 같이 구하면 훨씬 빠르게 구할 수 있습니다.
'Algorithm' 카테고리의 다른 글
| [알고리즘] 배낭 채우기 알고리즘(Knapsack Problem) (0) | 2023.08.25 |
|---|---|
| [알고리즘] 분리 집합 (0) | 2023.08.11 |
| [알고리즘] 위상 정렬 (0) | 2023.08.09 |
| [알고리즘] 플로이드 워셜 (0) | 2022.02.18 |
| [알고리즘] 벨만 포드(최단경로에 음수 간선이 있을 때) (0) | 2022.02.12 |
