https://www.acmicpc.net/problem/10159
10159번: 저울
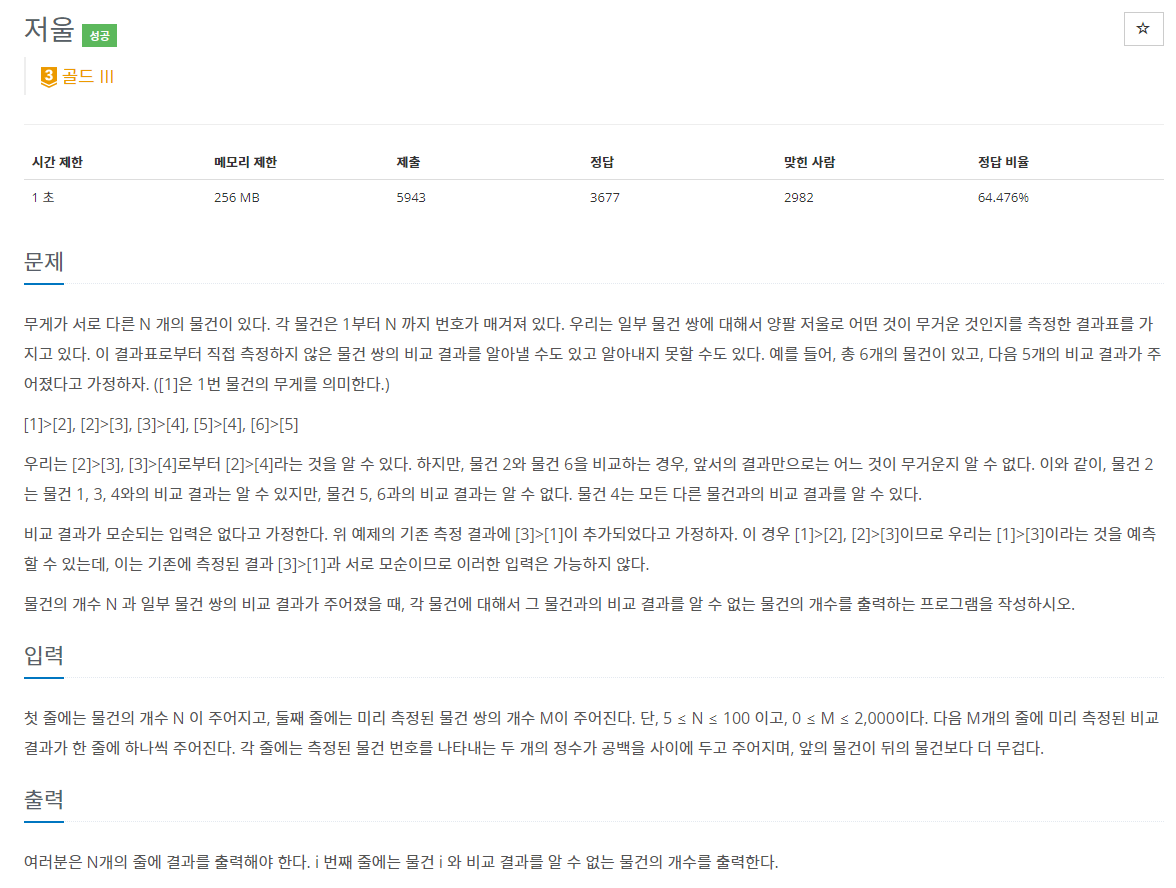
첫 줄에는 물건의 개수 N 이 주어지고, 둘째 줄에는 미리 측정된 물건 쌍의 개수 M이 주어진다. 단, 5 ≤ N ≤ 100 이고, 0 ≤ M ≤ 2,000이다. 다음 M개의 줄에 미리 측정된 비교 결과가 한 줄에 하나씩
www.acmicpc.net
풀이
플로이드 워셜 알고리즘을 사용해서 풀어주었다. 블로그 글 참고.
https://sunghyun98.tistory.com/66
[알고리즘] 플로이드 워셜
최단경로 알고리즘이며 모든 노드에서 모든 노드로부터 최단경로를 구할 때 사용하는 알고리즘이다. 플로이드 워셜 vs 다익스트라 저번 시간에 다뤘던 한 지점에서 모든 노드로의 최단경로를
sunghyun98.tistory.com
# 10159번 저울
# 플로이드 와샬 알고리즘 사용
import sys
input = sys.stdin.readline
INF = int(1e9)
n = int(input())
m = int(input())
graph = [[INF] * (n+1) for _ in range(n+1)]
for a in range(1, n+1):
for b in range(1, n+1):
if a == b:
graph[a][b] = 0
# 숫자가 들어가서 INF를 대체하면 아래서 숫자 비교가 가능하다는 뜻이다.
for _ in range(m):
a, b = map(int, input().split())
graph[a][b] = 1
for k in range(1, n+1):
for a in range(1, n+1):
for b in range(1, n+1):
graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b])
# 노드 a와 비교가 가능한 노드의 개수 cnt
for a in range(1, n+1):
cnt = 0
for b in range(1, n+1):
# 양쪽에서 비교가 불가능해야한다.
if graph[a][b] == INF and graph[b][a] == INF:
cnt += 1
print(cnt)출력결과

'백준 > 최단거리' 카테고리의 다른 글
| [백준] 10282번 해킹 - 파이썬 (0) | 2022.02.20 |
|---|---|
| [백준] 18352번 특정 거리의 도시 찾기 - 파이썬 (0) | 2022.02.19 |
| [백준] 1865번 웜홀 - 파이썬 (1) | 2022.02.17 |
| [백준] 1238번 파티 - 파이썬 (0) | 2022.02.12 |
| [백준] 11657번 타임머신 - 파이썬 (0) | 2022.02.12 |
https://www.acmicpc.net/problem/10159
10159번: 저울
첫 줄에는 물건의 개수 N 이 주어지고, 둘째 줄에는 미리 측정된 물건 쌍의 개수 M이 주어진다. 단, 5 ≤ N ≤ 100 이고, 0 ≤ M ≤ 2,000이다. 다음 M개의 줄에 미리 측정된 비교 결과가 한 줄에 하나씩
www.acmicpc.net

풀이
플로이드 워셜 알고리즘을 사용해서 풀어주었다. 블로그 글 참고.
https://sunghyun98.tistory.com/66
[알고리즘] 플로이드 워셜
최단경로 알고리즘이며 모든 노드에서 모든 노드로부터 최단경로를 구할 때 사용하는 알고리즘이다. 플로이드 워셜 vs 다익스트라 저번 시간에 다뤘던 한 지점에서 모든 노드로의 최단경로를
sunghyun98.tistory.com
# 10159번 저울
# 플로이드 와샬 알고리즘 사용
import sys
input = sys.stdin.readline
INF = int(1e9)
n = int(input())
m = int(input())
graph = [[INF] * (n+1) for _ in range(n+1)]
for a in range(1, n+1):
for b in range(1, n+1):
if a == b:
graph[a][b] = 0
# 숫자가 들어가서 INF를 대체하면 아래서 숫자 비교가 가능하다는 뜻이다.
for _ in range(m):
a, b = map(int, input().split())
graph[a][b] = 1
for k in range(1, n+1):
for a in range(1, n+1):
for b in range(1, n+1):
graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b])
# 노드 a와 비교가 가능한 노드의 개수 cnt
for a in range(1, n+1):
cnt = 0
for b in range(1, n+1):
# 양쪽에서 비교가 불가능해야한다.
if graph[a][b] == INF and graph[b][a] == INF:
cnt += 1
print(cnt)출력결과

'백준 > 최단거리' 카테고리의 다른 글
| [백준] 10282번 해킹 - 파이썬 (0) | 2022.02.20 |
|---|---|
| [백준] 18352번 특정 거리의 도시 찾기 - 파이썬 (0) | 2022.02.19 |
| [백준] 1865번 웜홀 - 파이썬 (1) | 2022.02.17 |
| [백준] 1238번 파티 - 파이썬 (0) | 2022.02.12 |
| [백준] 11657번 타임머신 - 파이썬 (0) | 2022.02.12 |
